Exercise 05 - Size optimization of trusses¶
We will optimize truss structures in this exercise. There is a prepared Python class for trusses called Truss and you can import it via from torchfem import Truss. The next cells show an example of how to use the truss class.
from math import log, sqrt
import torch
from torchfem import Truss
torch.set_default_dtype(torch.double)
The truss consists of nodes (tensor with shape Nx2), elements(integer tensor with shape Mx2), forces (tensor with shape Nx2) acting on nodes, constraints (boolean tensor with shape Nx2) defining for each degree of freedom wether it is constrained (True) or not (False), prescribed displacements (tensor with shape Nx2), cross section areas areas of each element (tensor with shape Mx1), and Young's moduli moduli of each element (tensor with shape Mx1). We can plot the object with Truss.plot().
# Define three nodes
nodes = torch.tensor([[0.0, 0.0], [1.0, 1.0], [2.0, 0.0]])
# Define two elements connecting nodes
elements = torch.tensor([[0, 1], [1, 2]])
# Create truss object
truss = Truss(nodes, elements)
# Define a single force downwards in x_2 direction
truss.forces[1, 1] = -0.25
# Constrain all DOFs except for the central node
truss.constraints[0, :] = True
truss.constraints[2, :] = True
# Properties of bars
truss.moduli[:] = 1.0
truss.areas[:] = 1.0
# Plot undeformend truss
truss.plot()
We can solve the truss problem for deformations at each node. This is done with a function Truss.solve(). The function returns displacements at each node u and forces at each node f.
We may compute stresses as as post-processing step via Truss.compute_stress(u), which returns the stress in each bar.
If we pass the displacements to the Truss.plot() function via (u=u), the visualization shows the deformed configuration. If we pass stresses via Truss.plot(sigma=sigma), the visualization shows color-coded stress in each bar.
# Compute the solution of the truss problem
u, f = truss.solve()
# Compute the stresses in each element
sigma = truss.compute_stress(u)
# Plot deformend truss
truss.plot(u=u)
# Plot deformend truss with stresses
truss.plot(u=u, sigma=sigma)
Task 1 - Solving a simple truss structure¶
Consider the three bar truss example from a previous exercise and the lecture example shown below. The coordinate origin is located at Node 1 now.
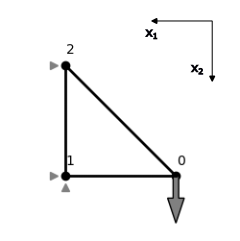
The truss is subjected to a force $P=-0.2$ indicated by the gray arrow and supports indicated by gray triangles. It has three nodes $$ \mathcal{N} = \{\mathbf{n}^0=(1,0)^\top, \mathbf{n}^1=(0,0)^\top,\mathbf{n}^2=(0,1)^\top \} $$ and three elements $$ \mathcal{E} = \{(\mathbf{n}^0, \mathbf{n}^1), (\mathbf{n}^0, \mathbf{n}^2), (\mathbf{n}^1, \mathbf{n}^2)\}. $$
Create a truss model named three_bar_truss representing this truss assuming $E=10.0$ and $A=1.0$ for each element.
a) Solve the truss problem and plot the truss in its deformed configuration with colors representing stresses in bars.
# Nodes
nodes = torch.tensor([[1.0, 0.0], [0.0, 0.0], [0.0, 1.0]])
# Elements
elements = torch.tensor([[0, 1], [0, 2], [1, 2]])
# Create truss
three_bar_truss = Truss(nodes, elements)
# Forces
three_bar_truss.forces = torch.zeros_like(nodes)
three_bar_truss.forces[0, 1] = -0.2
# Constraints
three_bar_truss.constraints[1, 0] = True
three_bar_truss.constraints[1, 1] = True
three_bar_truss.constraints[2, 0] = True
# Cross section design
three_bar_truss.areas[:] = 1.0
three_bar_truss.moduli[:] = 10.0
# Solve truss
u, f = three_bar_truss.solve()
sigma = three_bar_truss.compute_stress(u)
# Plot truss
three_bar_truss.plot(u=u, sigma=sigma)
b) Create a function named compute_lengths(truss) that accepts a truss object as input and returns a tensor containing the length of each element.
def compute_lengths(truss):
start_nodes = truss.nodes[truss.elements[:, 0]]
end_nodes = truss.nodes[truss.elements[:, 1]]
dx = end_nodes - start_nodes
return torch.linalg.norm(dx, dim=-1)
print(compute_lengths(three_bar_truss))
tensor([1.0000, 1.4142, 1.0000])
Task 2 - Bisection algorithm¶
To solve the dual problem when optimizing the truss cross sections, we will need to find the roots $\mu^*>0$ of the gradient $$ \frac{\partial \underline{\mathcal{L}}}{\partial \mu}(\mu) = \mathbf{l} \cdot \mathbf{x}^* (\mu) - V_0 = 0. $$
To prepare the search for these roots, you should implement a bisection algorithm. This algorithm performs well in this case of a highly non-linear convex optimization task, but in principle, you could also use any other gradient based algortihtm from previous exercises.
a) Write a function bisection(f, a, b, max_iter=50, tol=1e-10) that takes a function f, a bracket $[a,b]$ with $a<b$, an iteration limit max_iter and a tolerance for the solution tol. It should implement the following algorithm:
- While $b-a > tol$:
- $c = \frac{a+b}{2}$
- if $f(a)$ and $f(b)$ have the same sign, replace a with c
- else replace b with c
Break the loop, if the iteration count max_iter is exceeeded to prevent infinite loops.
def bisection(f, a, b, max_iter=50, tol=1e-10):
# Bisection method always finds a root, even with highly non-linear grad
i = 0
while (b - a) > tol:
c = (a + b) / 2.0
if i > max_iter:
raise Exception(f"Bisection did not converge in {max_iter} iterations.")
if f(a) * f(c) > 0:
a = c
else:
b = c
i += 1
return c
b) Test the function with the function $f(x)=x^3-\log(x)-5$.
def f(x):
return x**3 - log(x) - 5.0
root = bisection(f, 0.1, 10.0)
print(root)
1.7729093296358767
Task 3 - Optimization algorithm¶
a) Implement a truss optimization algorithm according to Example 27 in the lecture. To do so, define a function optimize(truss, a_0, a_min, a_max, V_0) taking a Truss object, an initial solution of a, bounds on a a_min and a_max as well as a maximum volume V_0. You may re-use code from the previous MMA exercise.
def optimize(truss, a_0, a_min, a_max, V_0, iter=10):
l = compute_lengths(truss)
k0 = truss.k() / truss.areas[:, None, None]
s = 0.7
L = []
a = [a_0]
# Iterate solutions
for k in range(iter):
# Solve the truss problem at point a_k
truss.areas = a[k]
u_k, f_k = truss.solve()
# Get strain energy of all truss elements for the given displacement
disp = u_k[truss.elements].reshape(-1, 4)
w_k = torch.max(
0.5 * torch.einsum("...i,...ij,...j", disp, k0, disp),
torch.zeros(len(truss.elements)),
)
# Compute lower asymptote
if k <= 1:
L.append(a[k] - s * (a_max - a_min))
else:
L_k = torch.zeros_like(L[k - 1])
osci = (a[k] - a[k - 1]) * (a[k - 1] - a[k - 2]) < 0.0
L_k[osci] = a[k][osci] - s * (a[k - 1][osci] - L[k - 1][osci])
L_k[~osci] = a[k][~osci] - 1 / sqrt(s) * (a[k - 1][~osci] - L[k - 1][~osci])
L.append(L_k)
# Compute lower move limit in this step
a_min_k = torch.max(a_min, 0.9 * L[k] + 0.1 * a[k])
# Analytical solution for a_star
def a_star(mu):
a_hat = L[k] + torch.sqrt((2 * w_k * (L[k] - a[k]) ** 2) / (mu * l))
return torch.clamp(a_hat, a_min_k, a_max)
# Analytical gradient
def grad(mu):
return torch.dot(a_star(mu), l) - V_0
# Solve dual problem
mu_star = bisection(grad, 1e-10, 100.0)
# Compute current optimal point with dual solution
a.append(a_star(mu_star))
return a
b) Test the optimization algorithm with the following code.
# Define initial solution and bounds
a_0 = torch.tensor([0.5, 0.2, 0.3])
a_min = 0.1 * torch.ones_like(a_0)
a_max = 1.0 * torch.ones_like(a_0)
# Define volume constraint
l = compute_lengths(three_bar_truss)
V0 = 0.5 * torch.dot(a_max, l)
# Optimize truss
a_opt = optimize(three_bar_truss, a_0, a_min, a_max, V0)
# Plot optimal solution
u, f = three_bar_truss.solve()
sigma = three_bar_truss.compute_stress(u)
three_bar_truss.plot(u=u, sigma=sigma, show_thickness=True)
c) Is the optimized truss a fully stressed design?
d) Compare the solution to the analytical solution from Exercise 3. Is it the same result?
Task 4 - Your own truss¶
a) Create your own truss problem by defining nodes, elements, forces and constraints to your liking.
n1 = torch.linspace(0.0, 4.0, 5)
n2 = torch.linspace(0.0, 1.0, 2)
n1, n2 = torch.stack(torch.meshgrid(n1, n2, indexing="xy"))
nodes = torch.stack([n1.ravel(), n2.ravel()], dim=1)
elements = torch.tensor(
[
[0, 1],
[1, 2],
[2, 3],
[3, 4],
[5, 6],
[6, 7],
[7, 8],
[8, 9],
[1, 5],
[0, 6],
[2, 6],
[1, 7],
[3, 7],
[2, 8],
[4, 8],
[3, 9],
[1, 6],
[2, 7],
[3, 8],
[4, 9],
]
)
my_truss = Truss(nodes, elements)
my_truss.forces[4, 1] = -0.1
my_truss.constraints[0, 0] = True
my_truss.constraints[0, 1] = True
my_truss.constraints[5, 0] = True
my_truss.areas[:] = 10.0
my_truss.moduli[:] = 1.0
my_truss.plot()
b) Solve your own truss for a prescribed distribution of cross-sectional areas. Plot the deformed truss with colored stresses.
u, f = my_truss.solve()
sigma = my_truss.compute_stress(u)
my_truss.plot(u=u, sigma=sigma)
c) Optimize the cross sections of your own truss.
# Define initial solution and bounds
a_0 = 5.0 * torch.ones((len(my_truss.elements)))
a_min = 1.0 * torch.ones_like(a_0)
a_max = 20.0 * torch.ones_like(a_0)
# Compute volume restriction
l = compute_lengths(my_truss)
V0 = 0.5 * torch.inner(a_max, l)
# Optimize
a_opt = optimize(my_truss, a_0, a_min, a_max, V0, iter=30)
# Plot result
u, f = my_truss.solve()
sigma = my_truss.compute_stress(u)
my_truss.plot(u=u, sigma=sigma, show_thickness=True)
d) What is the interpretation of bars having the minimum cross sectional area? What would happen if we set the minimum area to zero?
We can drop those bars from the design and we can essentially interpret this as a topology optimization. However, we cannot let them disappear completely, because that would make the stiffness matrix singular, as we cannot find a solution for the displacement of nodes connected to disappearing bars (e.g. Node 9 in this example).