4 Optimization using
local approximations
The optimization problems in the previous chapters utilized explicit
functions for the objective functions and constraints. However, in most
practical structural optimization problems, we are not able to formulate
such explicit functions. Instead, we use local approximations as a
remedy. These should be explicit convex functions that approximate the
structural problem in a local region well and are easy to solve at the
same time.
The procedure using a local approximation is as follows:
Choose a starting point \(\mathbf{x}^0\)
Evaluate the target function, constraints and their gradients at
the current position \(\mathbf{x}^k\).
Construct a local, explicit, and convex approximation \(\tilde{f}, \tilde{g}, \tilde{h}\) at \(\mathbf{x}^k\).
Solve the approximated optimization problem to find the next
point \(\mathbf{x}^{k+1}\).
Repeat steps 2, 3, and 4 until you reached a maximum number of
iteration \(k \le N\) or there is no
improvement anymore.
Note that during the optimization within each iteration, we use only
the approximation and do not have to evaluate the expensive target
function.
Learning Objectives
After studying this chapter and finishing the exercise, you should be
able to
approximate an optimization problem via Sequential Linear
Programming (SLP)
approximate an optimization problem via Sequential Quadratic
Programming (SQP)
approximate an optimization problem via Convex Linearization
(CONLIN)
approximate an optimization problem via the Method of Moving
Asymptotes (MMA)
discuss the relation between these approximation methods and
chose an appropriate method for a given task
4.1 Sequential linear
programming
In Sequential Linear Programming (SLP), we approximate the functions
in Equation at \(\mathbf{x}^k\) with
first order linear equations \[\begin{aligned}
\tilde{f}(\mathbf{x}) &= f(\mathbf{x}^k) + \nabla
f(\mathbf{x}^k) \cdot \left(\mathbf{x} - \mathbf{x}^k \right)
{\qquad(4.1)}\\
\tilde{g}_i(\mathbf{x}) &= g_i(\mathbf{x}^k) + \nabla
g_i(\mathbf{x}^k) \cdot \left(\mathbf{x} - \mathbf{x}^k \right)
{\qquad(4.2)}\\
\tilde{h}_j(\mathbf{x}) &= h_j(\mathbf{x}^k) + \nabla
h_j(\mathbf{x}^k) \cdot \left(\mathbf{x} - \mathbf{x}^k \right)
{\qquad(4.3)}\end{aligned}\] and limit the validity of the
approximation with so-called move limits \[\tilde{\mathbf{x}}^{-,k} \le \mathbf{x} \le
\tilde{\mathbf{x}}^{+,k}.{\qquad(4.4)}\] The resulting functions
are explicit linear expressions and the set for \(\mathbf{x}\) is compact, hence the
resulting problem is strictly convex. We limit the set because i) the
approximation is only valid close to \(\mathbf{x}^k\) and ii) the linear problem
requires a compact set to be strictly convex.
Example: SLP with move limits
We want to sequentially approximate the following quadratic function
\[f(\mathbf{x})= \mathbf{x} \cdot \mathbf{Q}
\cdot \mathbf{x} \quad \text{with} \quad \mathbf{x} \in \mathcal{R}^2
\quad \text{and} \quad
\mathbf{Q} =
\begin{pmatrix}
2 & 1 \\
1 & 1
\end{pmatrix}.{\qquad(4.5)}\] Obviously, this is
already an explicit convex function and we do not necessarily need to
employ an approximation to minimize a function like this. But for the
sake of this example, we assume that \(f(\mathbf{x})\) is a very complex function
with no explicit expression.
In this case we can get an explicit linear approximation \[\begin{aligned}
\tilde{f}(\mathbf{x}) = f(\mathbf{x}^k) + 2(\mathbf{Q} \cdot
\mathbf{x}^k) \cdot \left(\mathbf{x} - \mathbf{x}^k \right)
{\qquad(4.6)}\end{aligned}\] with an analytical expression for
the gradient. Then, a first approximation at \(\mathbf{x}^0=(1,1)^\top\) is \[\tilde{f}(\mathbf{x}) = 3 + \begin{pmatrix} 2\\1
\end{pmatrix} \cdot \left(\mathbf{x} - \mathbf{x}^k
\right).{\qquad(4.7)}\] Assuming a validity of \(\pm 0.5\) around the approximated point,
the move limits are \(\tilde{\mathbf{x}}^{-,0}=(0.5, 0.5)^\top\)
and \(\tilde{\mathbf{x}}^{+,0}=(1.5,
1.5)^\top\). An optimization with these conditions yields to the
next point \(\mathbf{x}^1=(0.5,0.5)^\top\) with \[\tilde{f}(\mathbf{x}) = 1.25 + \begin{pmatrix}
1\\0.5 \end{pmatrix} \cdot \left(\mathbf{x} - \mathbf{x}^k
\right){\qquad(4.8)}\] and with move limits \(\tilde{\mathbf{x}}^{-,1}=(0, 0)^\top\) and
\(\tilde{\mathbf{x}}^{+,1}=(1,
1)^\top\). An optimization under these conditions gives us the
final result \((0,0)^\top\) for the
minimum of the function \(f(\mathbf{x})\). We obtained this by
sequentially employing linear approximations and then performing
optimization on these approximations instead of the original "complex"
and expensive function.
4.2 Sequential quadratic
programming
In Sequential Quadratic Programming (SQP), we approximate the
objective function in Equation at \(\mathbf{x}^k\) with second order quadratic
equations \[\tilde{f}(\mathbf{x}) =
f(\mathbf{x}^k) + \nabla f (\mathbf{x}^k) \cdot \left(\mathbf{x} -
\mathbf{x}^k \right) + \frac{1}{2}\left(\mathbf{x} - \mathbf{x}^k
\right) \cdot \nabla^2 f(\mathbf{x}^k) \cdot \left(\mathbf{x} -
\mathbf{x}^k \right){\qquad(4.9)}\] and the restrictions with
first order linear approximations \[\begin{aligned}
\tilde{g}(\mathbf{x}) &= g(\mathbf{x}^k) + \nabla
g(\mathbf{x}^k) \left(\mathbf{x} - \mathbf{x}^k \right) {\qquad(4.10)}\\
\tilde{h}(\mathbf{x}) &= h(\mathbf{x}^k) + \nabla
h(\mathbf{x}^k) \left(\mathbf{x} - \mathbf{x}^k \right).
{\qquad(4.11)}\end{aligned}\] This results in a more accurate
approximation and also in a more balanced approximation, i.e. the same
approximation order for the roots of interest (for constraints we are
interested in roots of the function itself, for the objective we are
interest in the roots of the derivative). The Hessian \(\nabla^2 f\) may be approximated
efficiently using the BFGS algorithm. This way, the problem is convex
and we may use the methods from Chapter 3 to obtain the optimum.
4.3 Convex linearization
Both, SLP and SQP, can be applied for any non-linear optimization
problem. However, we can improve the approximation quality
significantly, if we leverage some knowledge about the fundamental
equation types seen in structural optimization.
Let’s consider an assembly of beams and design variables that
describe the cross sectional areas of the beams like in the last example
of Exercise 3. A property like volume or mass is linearly related to the
design variables and a linear approximation would be exact. Conversely,
stress and displacement are related to the inverse of the design
variable and we would need many sequential linear approximations to
approximate the inverse. However, this knowledge suggests that it would
be clever to substitute \(y_j =
x^{-1}_j\), which would lead to a exact approximations for
statically determined truss assemblies (Christensen and Klarbring 2008).
Then, our linear approximation becomes \[\tilde{f}(\mathbf{x}) = f(\mathbf{x}^k) + \sum_j
\frac{\partial f}{\partial y_j}(\mathbf{x}^k) \left(y_j(x_j) -
y_j(x^k_j) \right){\qquad(4.12)}\] for the objective function,
but obviously the same principles apply for constraints throughout the
remainder of this chapter. Employing the chain rule \[\frac{\partial f}{\partial y_j} (\mathbf{x}^k)
= \frac{\partial x_j}{\partial y_j}(\mathbf{x}^k) \frac{\partial
f}{\partial x_j} (\mathbf{x}^k)
= -(x^k_j)^2 \frac{\partial f}{\partial
x_j}(\mathbf{x}^k){\qquad(4.13)}\] this can be simplified to an
expression without \(y_j\) \[\tilde{f}(\mathbf{x}) = f(\mathbf{x}^k) + \sum_j
\frac{\partial f}{\partial x_j}(\mathbf{x}^k)
\underbrace{\frac{x^k_j}{x_j}}_{\Gamma_j} \left(x_j - x^k_j
\right).{\qquad(4.14)}\] The difference to the regular linear
approximation is only the term indicated with \(\Gamma_j\). Hence we can set \(\Gamma_j = 1\) for variables that should be
approximated linearly and set \(\Gamma_j =
x^k_j / x_j\) for variables that should be approximated
inversely. Instead of choosing the approximation for each variable
manually, we may use the the sign of the partial derivative and define
an approximation method as \[\begin{aligned}
\tilde{f}(\mathbf{x}) &= f(\mathbf{x}^k) + \sum_j \frac{\partial
f}{\partial x_j}(\mathbf{x}^k) \Gamma_j \left(x_j - x^k_j \right)
{\qquad(4.15)}\\
\Gamma_j &=
\begin{cases}
1 &\quad \text{if} \quad \frac{\partial f}{\partial x_j}
(\mathbf{x}^k) \ge 0 \\
\frac{x^k_j}{x_j} &\quad \text{if} \quad \frac{\partial
f}{\partial x_j} (\mathbf{x}^k) < 0.
\end{cases}
{\qquad(4.16)}\end{aligned}\] This method is termed Convex
Linearization or CONLIN (Fleury 1989). The CONLIN method provides
a convex separable optimization problem, hence the Lagrangian duality
method is a suitable solution method (Christensen and Klarbring
2008; Harzheim 2014).
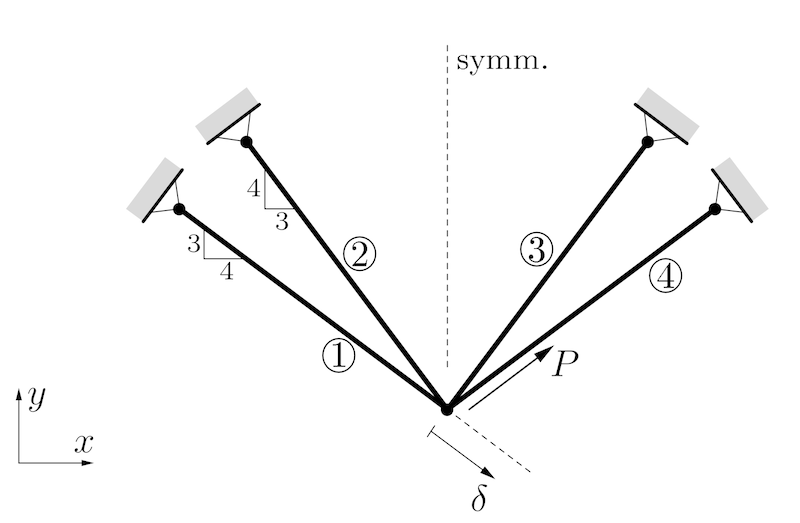
Example: CONLIN
The volume of a four-bar truss (Christensen and Klarbring 2008)
should be minimized under the displacement constraint \(\delta \le \delta_0\). There is a force
\(P>0\) and all bars have identical
lengths \(l\) and identical Young’s
moduli \(E\). The modifiable structural
variables are the cross sectional areas \(A_1=A_4\) and \(A_2=A_3\). We define \(A_0 = Pl / (10\delta_0E)\) and constrain
the variables \(0.2A_0 \le A_j \le 2.5
A_0\). Then we can use dimensionless design variables \(a_1=A_1/A_0 \in [0.2, 2.5]\) and \(a_2=A_2/A_0 \in [0.2, 2.5]\).
The optimization problem is \[\begin{aligned}
\min_{\mathbf{a}} \quad & f(\mathbf{a})= a_1 +
a_2{\qquad(4.17)}\\
\textrm{s.t.} \quad & g(\mathbf{a}) =
\frac{8}{16a_1+9a_2} - \frac{4.5}{9a_1+16a_2} - \delta_0 \le
0 {\qquad(4.18)}\\
\quad & \mathbf{a} \in [0.2,2.5]^2
{\qquad(4.19)}\end{aligned}\] This problem is not convex,
because the constraint \(g(\mathbf{a})\) (shown as solid black line
in the following plot for \(\delta_0=0.1\)) is not a convex function.
This leads to two local minima, one at \(a_2=0.2\) and one at \(a_2=2.5\).

The CONLIN approximation of the objective function is the objective
function itself - it is already linear. A CONLIN approximation of the
constraint function at \(\mathbf{a}^0=(2,1)^\top\) is computed using
automatic differentiation in PyTorch and results in the dashed black
line. The resulting problem is convex and can be solved, e.g. using
Lagrangian duality. The unique solution of this problem is the point
\(\mathbf{a}^1=(1.2,0.2)^\top\). We can
apply the CONLIN method again at this point to obtain a new convex
problem. Solving this problem gives \(\mathbf{x}^2=(0.85,0.2)^\top\), which is
close to the optimal solution \(\mathbf{a}^*\), but could be improved with
further iterations. Note that not every CONLIN approximation is
conservative, i.e. it can happen that \(\tilde{g}(\mathbf{a}) < g(\mathbf{a})\).
In that case, the solution will tend to oscillate around the optimal
point.
4.4 Method of Moving
Asymptotes
CONLIN is an effective method to turn structural optimization
problems into convex separable optimization tasks. However, it is
sometimes too conservative causing slow convergence or sometimes not
conservative enough causing no convergence at all. We could improve the
method by adjusting how conservative we approximate a function.
We may obtain an adjustable method by defining \[\tilde{f}(\mathbf{x}) = r(\mathbf{x}^k) + \sum_j
\left( \frac{p_{j}^k}{U^k_j-x_j} + \frac{q_{j}^k}{x_j-L^k_j} \right)
\label{eq:mma_start}{\qquad(4.20)}\] where \[\begin{aligned}
p_{j}^k &=
\begin{cases}
(U^k_j-x^k_j)^2 \frac{\partial f}{\partial x_j}
(\mathbf{x}^k) &\quad \text{if} \quad \frac{\partial f}{\partial
x_j} (\mathbf{x}^k) > 0 \\
0 &\quad \text{if} \quad \frac{\partial f}{\partial x_j}
(\mathbf{x}^k) \le 0.
\end{cases} {\qquad(4.21)}\\
q_{j}^k &=
\begin{cases}
0 &\quad \text{if} \quad \frac{\partial f}{\partial x_j}
(\mathbf{x}^k) \ge 0 \\
- (x^k_j-L^k_j)^2 \frac{\partial f}{\partial x_j} (\mathbf{x}^k)
&\quad \text{if} \quad \frac{\partial f}{\partial x_j}
(\mathbf{x}^k) < 0.
\end{cases} {\qquad(4.22)}\\
r(\mathbf{x}^k) &= f(\mathbf{x}^k) - \sum_j
\left(\frac{p_{j}^k}{U^k_j-x^k_j} + \frac{q_{j}^k}{x^k_j-L^k_j} \right)
\label{eq:mma_end}
{\qquad(4.23)}\end{aligned}\] with \(L^k_j < x_j < U^k_j\). The parameters
\(L^k_j\) and \(U_j^k\) are called the lower and upper
asymptotes, respectively. They can be adjusted ("move"), hence the
method is termed Method of Moving Asymptotes (MMA) (Svanberg 1987). It
can be proven that this is a generalization, as setting \(L^k_j \rightarrow 0\) and \(U^k_j \rightarrow \infty\) recovers the
CONLIN method and setting \(L^k_j \rightarrow
-\infty\) and \(U^k_j \rightarrow
\infty\) recovers the SLP method.
To prevent singularities by reaching the asymptotes, we use move
limits \[L^k_j < \tilde{x}_j^{-,k} \le x_j
\le \tilde{x}_j^{+,k} < U_j^k.{\qquad(4.24)}\] similar to SLP.
These could be chosen for example as \[\begin{aligned}
\tilde{x}_j^{-,k} &= \max(x^-_j, 0.9 L_j^k + 0.1 x_j^k)
{\qquad(4.25)}\\
\tilde{x}_j^{+,k} &= \min(x^+_j, 0.9 U_j^k + 0.1 x_j^k).
\label{eq:mma_move_limits}
{\qquad(4.26)}\end{aligned}\]
The advantage of these adjustable asymptotes is that we can bring the
asymptotes closer to the current approximation \(\mathbf{x}^k\) to obtain a more
conservative approximation and move them further away to accelerate
convergence speed. But how do we chose the asymptotes? Svanberg (Svanberg 1987)
suggested the following heuristic approach:
In the first two iterations, set \[\begin{aligned}
L_j^k &= x_j^k - s (x^+_j - x^-_j) {\qquad(4.27)}\\
U^k_j &= x_j^k + s (x^+_j - x^-_j)
{\qquad(4.28)}\end{aligned}\] with \(s
\in (0,1)\).
For the following iterations (\(k>1\)) check for each design variable,
if it oscillates. If it oscillates, i.e. \((x_j^k-x_j^{k-1})(x_j^{k-1}-x_j^{k-2}) <
0\), bring asymptotes closer to \(x_j^k\) by \[\begin{aligned}
\label{eq:mma_heuristic_first}
L_j^k &= x_j^k - s (x_j^{k-1} - L_j^{k-1})
{\qquad(4.29)}\\
U_j^k &= x_j^k + s (U_j^{k-1} - x_j^{k-1}).
{\qquad(4.30)}\end{aligned}\]
If the solution does not oscillate, i.e. \((x_j^k-x_j^{k-1})(x_j^{k-1}-x_j^{k-2}) \ge
0\), move the asymptotes further away from \(x_j^k\) by \[\begin{aligned}
L_j^k &= x_j^k - \frac{1}{\sqrt{s}} (x_j^{k-1} -
L_j^{k-1}) {\qquad(4.31)}\\
U_j^k &= x_j^k + \frac{1}{\sqrt{s}} (U_j^{k-1} -
x_j^{k-1}).
\label{eq:mma_heuristic_last}
{\qquad(4.32)}\end{aligned}\]
Svanbergs original version uses the same asymptotes \(L_j^k\) and \(U_j^k\) for the objective function and
constraints. There is also a method termed Generalized Method of
Moving Asymptotes (GMMA) (Zhang and Fleury 1997) that uses
different asymptotes for each function. However, this requires a more
complicated heuristic to obtain such asymptotes.
Example: MMA
Consider the previous example with the optimization problem \[\begin{aligned}
\min_{\mathbf{a}} \quad & f(\mathbf{a})= a_1 +
a_2{\qquad(4.33)}\\
\textrm{s.t.} \quad & g(\mathbf{a}) =
\frac{8}{16a_1+9a_2} - \frac{4.5}{9a_1+16a_2} -0.1 \le
0 {\qquad(4.34)}\\
\quad & \mathbf{a} \in [0.2,2.5]^2
{\qquad(4.35)}\end{aligned}\]
A MMA approximation at \(\mathbf{a}^0=(2,1)^\top\) is illustrated in
the following image with the dashed line for \(s_0=0.2\).
If we chose \(s_0=0.5\), we get a
less conservative approximation, as shown in the next image. This
results in faster convergence, as an optimization of the convex problem
gets closer to the optimum in a single step.
This example shows just the first iteration - the full method would
require sequential approximation and optimization with the Lagrangian
duality method until convergence. During each iteration, we would use
the heuristic given in Equations 4.29 to 4.32 to update asymptotes.
References
Christensen, Peter W., and Anders Klarbring. 2008. An Introduction to Structural Optimization.
Springer Netherlands.
Fleury, C. 1989. “CONLIN: An efficient dual
optimizer based on convex approximation concepts.”
Structural Optimization 1: 81–89.
Harzheim, Lothar. 2014. Strukturoptimierung,
Grundlagen und Anwendungen. Europa Lehrmittle.
Svanberg, Krister. 1987. “The Method of Moving Asymptotes—a New
Method for Structural Optimization.” International Journal
for Numerical Methods in Engineering 24 (2): 359–73.
Zhang, Wei-Hong, and C. Fleury. 1997. “A Modification of Convex
Approximation Methods for Structural Optimization.” Computers
& Structures 64 (1): 89–95.
